- New
-
Topics
- All Categories
- Metaphysics and Epistemology
- Value Theory
- Science, Logic, and Mathematics
- Science, Logic, and Mathematics
- Logic and Philosophy of Logic
- Philosophy of Biology
- Philosophy of Cognitive Science
- Philosophy of Computing and Information
- Philosophy of Mathematics
- Philosophy of Physical Science
- Philosophy of Social Science
- Philosophy of Probability
- General Philosophy of Science
- Philosophy of Science, Misc
- History of Western Philosophy
- Philosophical Traditions
- Philosophy, Misc
- Other Academic Areas
- Journals
- Submit material
- More
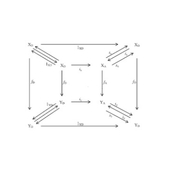
Functorial Semantics for the Advancement of the Science of Cognition
Mind and Matter 15 (2):161–184 (2017)
Abstract
Our manuscript addresses the foundational question of cognitive science: how do we know? Specifically, examination of the mathematics of acquiring mathematical knowledge revealed that knowing-within-mathematics is reflective of knowing-in-general. Based on the correspondence between ordinary cognition (involving physical stimuli, neural sensations, mental concepts, and conscious percepts) and mathematical knowing (involving objective particulars, measured properties, abstract theories, and concrete models), we put forward the functorial semantics of mathematical knowing as a formalization of cognition. Our investigation of the similarity between mathematics and cognition led us to argue against the compartmentalization of scientific knowledge and ordinary cognition, and make a case for the understanding of the basic science of knowing in terms of functorial semantics. Recognizing functorial semantics as an elementary form of cognition can help advance cognitive science the way calculus helped in the advancement of physics.Author Profiles
Other Versions
No versions found
My notes
Similar books and articles
Functorial Semantics for the Advancement of the Science of Cognition.Venkata Posina, Dhanjoo N. Ghista & Sisir Roy - 2017 - Mind and Matter 15 (2):161-184.
Isbell Conjugacy for Developing Cognitive Science.Venkata Rayudu Posina, Posina Venkata Rayudu & Sisir Roy - manuscript
Distributed cognition without distributed knowing.Ronald N. Giere - 2007 - Social Epistemology 21 (3):313-320.
Metaphor and the Philosophical Implications of Embodied Mathematics.Bodo Winter & Jeff Yoshimi - 2020 - Frontiers in Psychology 11.
F. William Lawvere. Functorial semantics of algebraic theories. Proceedings of the National Academy of Sciences of the United States of America, vol. 50 , pp. 869–872. [REVIEW]Calvin C. Elgot - 1974 - Journal of Symbolic Logic 39 (2):340-341.
Truth through Nonviolence.Venkata Rayudu Posina - 2016 - GITAM Journal of Gandhian Studies 5 (1):143-150.
A Cognitive Approach to Benacerraf's Dilemma.Luke Jerzykiewicz - 2009 - Dissertation, University of Western Ontario
Analytics
Added to PP
2024-03-06
Downloads
219 (#123,359)
6 months
98 (#70,641)
2024-03-06
Downloads
219 (#123,359)
6 months
98 (#70,641)
Historical graph of downloads
Author Profiles
References found in this work
Concepts: Where Cognitive Science Went Wrong.Jerry A. Fodor - 1998 - Oxford, GB: Oxford University Press.
The unreasonable effectiveness of mathematics in the natural sciences.Eugene Wigner - 1960 - Communications in Pure and Applied Mathematics 13:1-14.
The Mind Doesn't Work That Way: The Scope and Limits of Computational Psychology.Jerry Fodor - 2001 - Philosophical Quarterly 51 (205):549-552.